나이브 베이즈
지도 학습 알고리즘으로써 주로 분류의 목적으로 사용
속성들 사이의 독립을 가정하는 베이즈 정리를 기반으로 함.
베이즈 정리
사전 확률의 정보를 이용해 사후 확률을 추정
사전 확률 : 원인인 사전 확률
사후 확률 : 결과가 발생했다는 조건에서 원인이 발생했을 확률
조건부확률
P(B|A) 사건 A가 일어난 상태에서 사건 B가 일어날 확률
우도 (Likelihood)
원인이 발생했다는 조건에서 결과가 발생했을 확률
라플라스 스무딩 (Laplace Smoothing)
학습벡터에 제시되어 있지 않은 요소가 있는 새로운 입력 벡터
조건부 확률이 -이 되어 정상적으로 분류가 되지 않는 경우를 방지하기 위해 확률 값을 보정하는데 사용된다.
로그(Log) 변환
확률은 항상 1보다 작은 값을 갖는 특성을 갖고 있다.
입력벡터를 구성하는 요소가 많을 수록 입력 벡터에 대한 각각의 조건부확률이 매우 낮아짐 -> 조건부 확률 값 비교 불가 (Underflow)
Underflow 현상을 해결하기 위해 조건부 확률 계산식에 log를 적용
예제를 이용한 Naive Bayes
예제 데이터 : 날씨, 온도, 습도에 따른 테니스 경기 여부를 나타내는 tennis 데이터
과정
예제 데이터 -> 빈도 테이블/우도 테이블 생성 -> 나이브 베이즈 방정식을 사용하여 각 클래스의 사전확률 계산 -> 입력 벡터에 대한 사후 확률 계산
계산된 사후 확률 중 가장 높은 사후 확률을 갖는 클래스 : 입력 벡터에 대한 예측 결과
학습 벡터 : Outlook(Sunny, Overcast, Rain), Temperature(Hot, Cool, Mild), Humidity(High, Normal)
클래스 : PlayTennis (No, Yes)
예제 데이터

1. Outlook 벡터에 대한 빈도 테이블 생성
Sunny 5 Overcast 4 Rain 5 -> 전체 요소 14 ----- 클래스의 요소 No Yes에 하나씩 대응 No 5 Yes 9
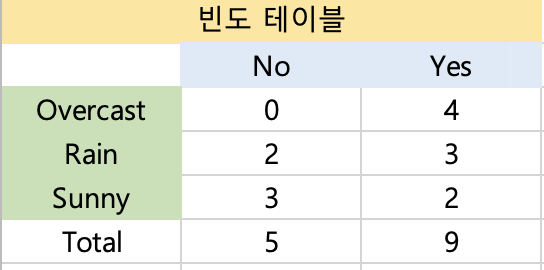
2. 빈도 테이블을 이용하여 우도 테이블 생성
P(Overcast) Overcast의 사전 확률 : Overcast/Oulook벡터 전체 요소 = 4/14 = 0.29
P(Rain) Rain의 사전 확률 : Rain/Oulook벡터 전체 요소 = 5/14 = 0.36
P(Sunny) Sunny의 사전 확률 : Sunny/Oulook벡터 전체 요소 = 5/14 = 0.36 
3. 클래스 요소에 대한 사전 확률
P(No) No 수 / 클래스 전체 요소 = 5/14 = 0.36
P(Yes) Yes 수 / 클래스 전체 요소 = 9/14 = 0.644. 우도
P(Overcast|Yes) = 4/9 = 0.55
P(Rain|No) = 2/5 = 0.4
P(Rain|Yes) = 3/9 = 0.33
P(Sunny|No) = 3/5 = 0.5
P(Sunny|Yes) = 2/9 = 0.22
5. 사후 확률
P(No|Sunny) = { P(No)P(Suuny|No) } / P(Sunny) = 0.36 * 0.6 / 0.36 = 0.6
P(No|Rain) = { P(No)P(Rain|No) } / P(Rain) = 0.36 * 0.4 / 0.36 = 0.4
6. 새로운 입력 벡터와 클래스에 대한 사후 확률
X(새로운 입력 벡터) = (Outlook = Rain, Temperature = Cool, Humidity = Normal)
- 클래스 No일 때, 입력 벡터 X의 우도
: No가 발생했다는 조건에서, Outlook=Rain * Temperature=Cool * Humidity=Normal
= P(X|NO) = P(Outlook=Rain|Class=No) * P(Temperature=Cool|Class=No) * P(Humidity=Noraml|Class=No)
= 0.4 * 0.2 * 0.2 = 0.016 - 클래스 Yes일 때, 입력 벡터 X의 우도
: Yes가 발생했다는 조건에서, Outlook=Rain * Temperature=Cool * Humidity=Normal
= P(X|Yes) = P(Outlook=Rain|Class=Yes) * P(Temperature=Cool|Class=Yes) * P(Humidity=Noraml|Class=Yes)
= 0.33 * 0.33 * 0.67 = 0.073 - 입력벡터 X가 발생했을 때, No가 발생했을 사후 확률
P(No|X) = { P(No)P(X|No) } / P(X) = 0.36 * 0.016 / 0.36 * 0.29 * 0.5 = 0.00576 / 0.052 = 0.1107 - 입력벡터 X가 발생했을 때, Yes가 발생했을 사후 확률
P(Yes|X) = { P(Yes)P(X|Yes) } / P(X) = 0.64 * 0.073 / 0.36 * 0.29 * 0.5 = 0.04672 / 0.052 = 0.8984
사후 확률을 비교해보면, Yes가 더 큰 것을 알 수 있음
P(No|X) < P(Yes|X) => Class = Yes
python 코드
from statistics import fmean
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
import pandas as pd
import numpy as np
# 예제 데이터 로드
tennis_data = pd.read_csv('playtennis.csv')
# 데이터 전처리
tennis_data.Outlook = tennis_data.Outlook.replace('Sunny',0)
tennis_data.Outlook = tennis_data.Outlook.replace('Overcast',1)
tennis_data.Outlook = tennis_data.Outlook.replace('Rain',2)
tennis_data.Temperature = tennis_data.Temperature.replace('Hot',3)
tennis_data.Temperature = tennis_data.Temperature.replace('Mild',4)
tennis_data.Temperature = tennis_data.Temperature.replace('Cool',5)
tennis_data.Humidity = tennis_data.Humidity.replace('High',6)
tennis_data.Humidity = tennis_data.Humidity.replace('Normal',7)
tennis_data.Wind = tennis_data.Wind.replace('Weak',8)
tennis_data.Wind = tennis_data.Wind.replace('Strong',9)
tennis_data.PlayTennis = tennis_data.PlayTennis.replace('No',10)
tennis_data.PlayTennis = tennis_data.PlayTennis.replace('Yes',11)
# 데이터 분리
X = np.array(pd.DataFrame(tennis_data, columns = ['Outlook','Temperature','Humidity','Wind']))
y = np.array(pd.DataFrame(tennis_data, columns = ['PlayTennis']))
# Train, Test Set 구성
X_train, X_test, y_train, y_test = train_test_split(X, y)
# Naive Bayes 모델 생성
gnb_clf = GaussianNB()
gnb_clf = gnb_clf.fit(X_train, y_train)
# 클래스 예측
gnb_prediction = gnb_clf.predict(X_test)
# 예측 클래스 확인
print(gnb_prediction)
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import f1_score
from sklearn.metrics import accuracy_score
# 얘측 값과 실제값 비교 confusion matrix
print('Confusion Matrix')
print(confusion_matrix(y_test, gnb_prediction))
# 얘측 값과 실제값 비교 classification report
print('Classification Report')
print(classification_report(y_test, gnb_prediction))
# weight 클래스 별로 가중치 적용하는 역할, true 정확도 계산해서 출력해주는 역할
fmeasure = round(f1_score(y_test, gnb_prediction, average = 'weighted'), 2)
accuracy = round(accuracy_score(y_test, gnb_prediction, normalize = True), 2)
# 데이터 프레임 형태로 출력
df_nbclf = pd.DataFrame(columns=['Classifier','F-Measure','Accuracy'])
df_nbclf.loc[len(df_nbclf)] = ['Naive Bayes', fmeasure, accuracy]
df_nbclf
'데이터 > 머신러닝' 카테고리의 다른 글
| 기계학습 (0) | 2022.06.29 |
|---|---|
| 적대적 머신러닝 - 학습 알고리즘 공격 모델 (0) | 2022.06.29 |
| 적대적 머신러닝 - 시큐어 학습을 위한 프레임워크 (0) | 2022.06.29 |
| 적대적 머신러닝 (0) | 2022.06.28 |
